
Series and parallel resistors
In this section we deal with the
mathematics of more than one resistor in a series or parallel circuit.
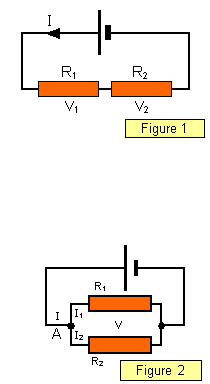
Two resistors in series (Figure 1)
The current (I) flowing through R
1 and R
2 is the same
and so the potential differences across them are V
1 = IR
1 and
V
2 = IR
2 But using Kirchoff's second rule the total
potential difference across them is
V = V
1 +
V
2
Therefore V = IR = IR
1 + IR
2 where R is the effective series resistance of the two resistors.
So:
Resistors in series: R = R1 + R2
Two resistors in parallel (Figure 2)
The potential difference (V)
across each of the two resistors is the same, and the current (I) flowing into junction A is
equal to the sum of the currents in the two branches (Kirchoff's first rule) therefore:
I =
I
1 + I
2But since V =
I
1R
1 = I
2R
2 I = V/R =
V/R
1 + V/R
2
Resistors in parallel: 1/R = 1/R1 + 1/R2
where R is the effective
resistance of the two resistors in parallel.
Notice that two resistors in series always have a larger effective resistance than either of the two resistors on their own, while two in
parallel always have a lower resistance. This means that connecting two or more resistors in
parallel, such as the use of a mains adaptor, will increase the current drawn from a supply
(Look at the section that deals with the bath with the two plug holes!).
Example problems
1. Calculate the resistance of the following combinations:
(a) 100 W and 50 W in series
(b) 100 W and 50 W in parallel
(a) R = R1 + R2 = 100 + 50 = 150 W
(b) 1/R = 1/R1 + 1/R2 = 1/100 + 1/50 = and so R = 33 W
2. Calculate the current flowing through the following when a p.d of 12V is applied across the ends:
(a) 200 W and 1000 W in series
(b) 200 W and 1000 W in parallel
(a) resistance = 1200 W. Using I = V/R = 12/1200 = 0.01 A = 10 mA
(b) resistance = 167 W. Using I = V/R = 12/167 = 0.072 A = 72 mA
3. You are given one 100 W resistor and two 50 W resistors. How would you connect any combination of them to give a combined resistance of: (a) 200 W (b) 125 W
(a) 100 W in series with both the 50 W .
(b) the two 50 W in parallel and this in series with the 100 W
For three resistors in
series the combined resistance is:
R = R1 + R2 + R3
and for three resistors in parallel it is:
1/R = 1/R1 + 1/R2 + 1/R3
Resistors in parallel –
an alterative formula
The formula for two resistors in parallel may also be
written as:
R = R1R2/[R1 + R2]
N.B – this version
cannot be extended simply to cover the case of three resistors in parallel.
The
version for three resistors being: R =
R
1R
2R
3/[R
1R
2
+ R
1R
3 +
R
2R
3]
Example problems
1. Calculate the combined resistance of a 50 W and a 100 W resistor connected first in (a) series and then (b) in parallel
(a) Series resistance = 50 + 100 = 150 W
(b) Parallel resistance = 50x100/[50+100] = 5000/150 = 33.3 W
2. Calculate the combined resistance of two 50 W resistors connected in parallel, the combination being joined in series to a further 50 W resistor.
Parallel section resistance = 25 W
Then in series with a further 50 W giving a total resistance of 75 W.
A further note on circuits
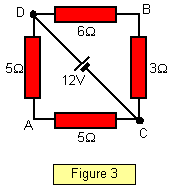
The p.d. between the points A and B in the circuit in Figure 3 may be found by
considering the ratio of the voltage drops in the resistors in each branch of the circuit. If the
potential at C is zero then:
Since the total resistance between D and C is 10? the
potential difference across the 5 O resistor = (5/10)x12 = 6V
Therefore potential at A =
6V
Potential drop through the 6O resistor = (6/9)x12 = 8V
Therefore potential at B =
4V
And so the potential difference between A and B = 6 - 4 = 2V
Some other interesting resistor networks may be found in
the following file:
Resistance networks
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB




 The p.d. between the points A and B in the circuit in Figure 3 may be found by
considering the ratio of the voltage drops in the resistors in each branch of the circuit. If the
potential at C is zero then:
The p.d. between the points A and B in the circuit in Figure 3 may be found by
considering the ratio of the voltage drops in the resistors in each branch of the circuit. If the
potential at C is zero then: